Statistik-Übungen: Häufigkeitsverteilungen und Kennzahlen
Eingeordnet in Mathematik
Geschrieben am in  Deutsch mit einer Größe von 17,39 KB
Deutsch mit einer Größe von 17,39 KB
1. Personenbefragung zur Anzahl der Personen zu Hause
Aufgabe: Stellen Sie eine Tabelle der absoluten und relativen Häufigkeiten dar und zeichnen Sie die Verteilung.
Lösung:
a) Tabelle der Häufigkeiten:

b) Verteilung der absoluten Häufigkeiten:

2. Umfrage zur Anzahl der Telefone pro Haushalt
Aufgabe: Stellen Sie eine Tabelle der absoluten und relativen Häufigkeiten dar und zeichnen Sie die Verteilung.
Lösung:
a) Tabelle der Häufigkeiten:

b) Verteilung der absoluten Häufigkeiten:

3. Ergebnisse eines Multiple-Choice-Tests
Aufgabe: Fassen Sie die Daten in einer Tabelle der absoluten und relativen Häufigkeiten zusammen und erstellen Sie ein Diagramm der Verteilung.
Lösung:
a) Tabelle der Häufigkeiten:

b) Diagramm der Verteilung:

4. Sportliche Aktivität pro Woche
Aufgabe: Stellen Sie eine Tabelle der absoluten und relativen Häufigkeiten dar und zeichnen Sie die Verteilung.
Lösung:
a) Tabelle der Häufigkeiten:

b) Verteilung der absoluten Häufigkeiten:

5. Ergebnisse von 20 Würfelwürfen
Aufgabe: Sortieren Sie die Daten in einer Tabelle der absoluten und relativen Häufigkeiten und zeichnen Sie die Verteilung.
Lösung:
a) Tabelle der Häufigkeiten:

b) Verteilung der absoluten Häufigkeiten:

6. Sprintzeiten von Teilnehmern
Aufgabe: Erstellen Sie eine Häufigkeitstabelle mit Intervallen der Länge 1, beginnend bei 8, und erstellen Sie ein Diagramm der Verteilung.
Lösung:
a) Häufigkeitstabelle:
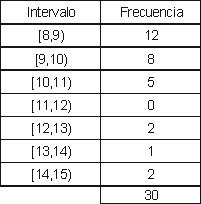
b) Diagramm der Verteilung:

7. Wochenstunden für das Studium
Aufgabe: Sortieren Sie die Daten in einer Frequenz-Tabelle mit Intervallen der Länge 3, beginnend bei 0, und erstellen Sie ein Diagramm der Verteilung.
Lösung:
a) Frequenz-Tabelle:
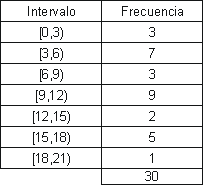
b) Diagramm der Verteilung:

8. Körpergröße von 30 Personen
Aufgabe: Erstellen Sie eine Häufigkeitstabelle mit Intervallen der Länge 5, beginnend bei 146,5, und erstellen Sie ein Diagramm der Verteilung.
Lösung:
a) Häufigkeitstabelle:
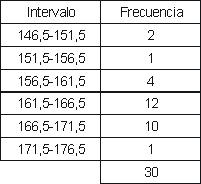
b) Diagramm der Verteilung:

9. Alter von 30 Personen
Aufgabe: Erstellen Sie eine Häufigkeitstabelle mit Intervallen der Länge 5, beginnend bei 0, und erstellen Sie ein Diagramm der Verteilung.
Lösung:
a) Häufigkeitstabelle:

b) Diagramm der Verteilung:

10. Gewicht von 30 Kindern
Aufgabe: Erstellen Sie eine Häufigkeitstabelle mit Intervallen der Länge 3, beginnend bei 24,5, und erstellen Sie ein Diagramm der Verteilung.
Lösung:
a) Häufigkeitstabelle:

b) Diagramm der Verteilung:

11. Notenverteilung in einem Mathematiktest
Aufgabe: Finden Sie den Mittelwert und die Standardabweichung.

Lösung:
Der Klassenmittelwert beträgt 6,1, mit einer Standardabweichung von 2,27.

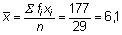


12. Fahrzeit zur Schule mit dem Schulbus
Aufgabe: Berechnen Sie den Mittelwert und die Standardabweichung dieser Verteilung.

Lösung:
Wir berechnen die Klassenmittelpunkte und erstellen die Tabelle:
Die Studenten benötigen im Durchschnitt 9,17 Minuten, mit einer Standardabweichung von 6,03 Minuten.


13. Anzahl der Personen pro Haushalt in 50 Familien
Aufgabe: Finden Sie den Mittelwert und die Standardabweichung.

Lösung:
Der durchschnittliche Anzahl der Personen, die im Haushalt leben, ist 3,1, mit einer Standardabweichung von 1,1 Personen.

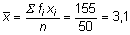


14. Altersverteilung
Aufgabe: Finden Sie den Mittelwert und die Standardabweichung für die folgende Altersverteilung.

Lösung:
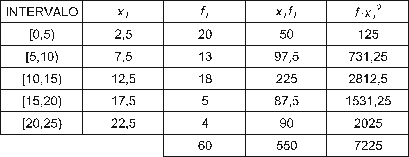
Wir berechnen die Klassenmittelpunkte und erstellen die Tabelle:

Das Durchschnittsalter beträgt 15,5 Jahre mit einer Standardabweichung von 6,71 Jahren.


15. Ergebnisse von 100 Würfelwürfen
Aufgabe: Finden Sie den Mittelwert und die Standardabweichung.

Lösung:
Wir haben eine Durchschnittsnote von 3,8 mit einer Standardabweichung von 1,75 Punkten erreicht.

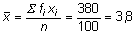


16. Vergleich der Notenverteilung zweier Klassen (A und B)
Aufgabe: Berechnen Sie den Variationskoeffizienten und vergleichen Sie die Verteilung der beiden Gruppen.
Lösung:
Klasse A: Mittelwert = 5,5, Standardabweichung = 2,1. Variationskoeffizient = (2,1 / 5,5) * 100% ≈ 38,18%.
Klasse B: Mittelwert = 7,3, Standardabweichung = 2,6. Variationskoeffizient = (2,6 / 7,3) * 100% ≈ 35,62%.
Klasse A weist eine größere relative Streuung der Noten auf als Klasse B.

17. Vergleich der Lohnverteilung zweier Unternehmen (A und B)
Aufgabe: Berechnen Sie den Variationskoeffizienten und sagen Sie, welches Unternehmen eine größere relative Änderung der Löhne aufweist.
Lösung:
Unternehmen A: Mittelwert = 900 €, Standardabweichung = 100 €. Variationskoeffizient = (100 / 900) * 100% ≈ 11,11%.
Unternehmen B: Mittelwert = 980 €, Standardabweichung = 150 €. Variationskoeffizient = (150 / 980) * 100% ≈ 15,31%.
Unternehmen B hat eine größere relative Änderung der Löhne.

18. Vergleich der Gewichtsverteilung zweier Tierarten (A und B)
Aufgabe: Berechnen Sie den Variationskoeffizienten und sagen Sie, welche der beiden Arten eine größere relative Veränderung der Gewichte aufweist.
Lösung:
Tierart A: Mittelwert = 21,3 kg, Standardabweichung = 2,5 kg. Variationskoeffizient = (2,5 / 21,3) * 100% ≈ 11,74%.
Tierart B: Mittelwert = 125 kg, Standardabweichung = 13 kg. Variationskoeffizient = (13 / 125) * 100% = 10,4%.
Tierart A weist eine größere relative Veränderung der Gewichte auf.

19. Anzahl der erworbenen Bücher pro Person
Aufgabe: Berechnen Sie den Median (I), das erste Quartil (Q1), das dritte Quartil (Q3) und das 80. Perzentil (P80).

Lösung:
Wir erstellen eine kumulative Häufigkeitstabelle:

Median (I) = 2 Bücher.
Q1 = 1 Buch.
Q3 = 3 Bücher.
P80 = 4 Bücher.
50% der Menschen haben 2 Bücher oder weniger erworben, und die restlichen 50% haben 2 oder mehr Bücher gekauft. Ähnlich interpretiert:


20. Anzahl der Würfe bis zum ersten Kopf
Aufgabe: Berechnen Sie den Median (I), das erste Quartil (Q1), das dritte Quartil (Q3) und das 30. Perzentil (P30).

Lösung:
Wir erstellen eine kumulative Häufigkeitstabelle:

Median (I) = 2 Würfe.
Q1 = 1 Würfe.
Q3 = 3 Würfe.
P30 = 2 Würfe.
50% der Zeit wurden 2 oder weniger Würfe benötigt, und die restlichen 50% benötigten 2 oder mehr Würfe. Ähnlich interpretiert:


21. Ergebnisse von 120 Würfelwürfen
Aufgabe: Berechnen Sie den Median (I), das erste Quartil (Q1), das dritte Quartil (Q3) und das 20. Perzentil (P20).

Lösung:
Wir erstellen eine kumulative Häufigkeitstabelle:

Median (I) = 3.
Q1 = 2.
Q3 = 4.
P20 = 2.
50% der Zeit wurde eine Augenzahl von 3 oder weniger erzielt, und 50% der Zeit wurde eine Augenzahl von 3 oder mehr erzielt. Ähnlich interpretiert:


22. Erreichte Punktzahlen von Athleten bei einem Sportereignis
Aufgabe: Berechnen Sie den Median (I), das erste Quartil (Q1) und das dritte Quartil (Q3).

Lösung:
Wir erstellen eine kumulative Häufigkeitstabelle:

Median (I) = 4 Punkte.
Q1 = 3 Punkte.
Q3 = 5 Punkte.
50% der Athleten erzielten eine Punktzahl von 4 oder weniger, und 50% erzielten eine Punktzahl von 4 oder mehr. Ähnlich interpretiert:


23. Datenanalyse
Aufgabe: Berechnen Sie den Median (I), das erste Quartil (Q1), das dritte Quartil (Q3) und das 90. Perzentil (P90).

Lösung:
Wir erstellen eine kumulative Häufigkeitstabelle:

Median (I) = 5.
Q1 = 3.
Q3 = 7.
P90 = 9.

